Union-Find Set / Disjoint Set Union 并查集介绍

December 02, 2021 8153

开篇废话

数据结构「并查集」（Union-Find），也称「不相交集合」（Disjoin-Sets）挺火的，刷题的时候一直遇到，刷到必是medium以上。本身原理并不复杂，就是实现代码稍微多了点。

原理

并查集主要知识点导图

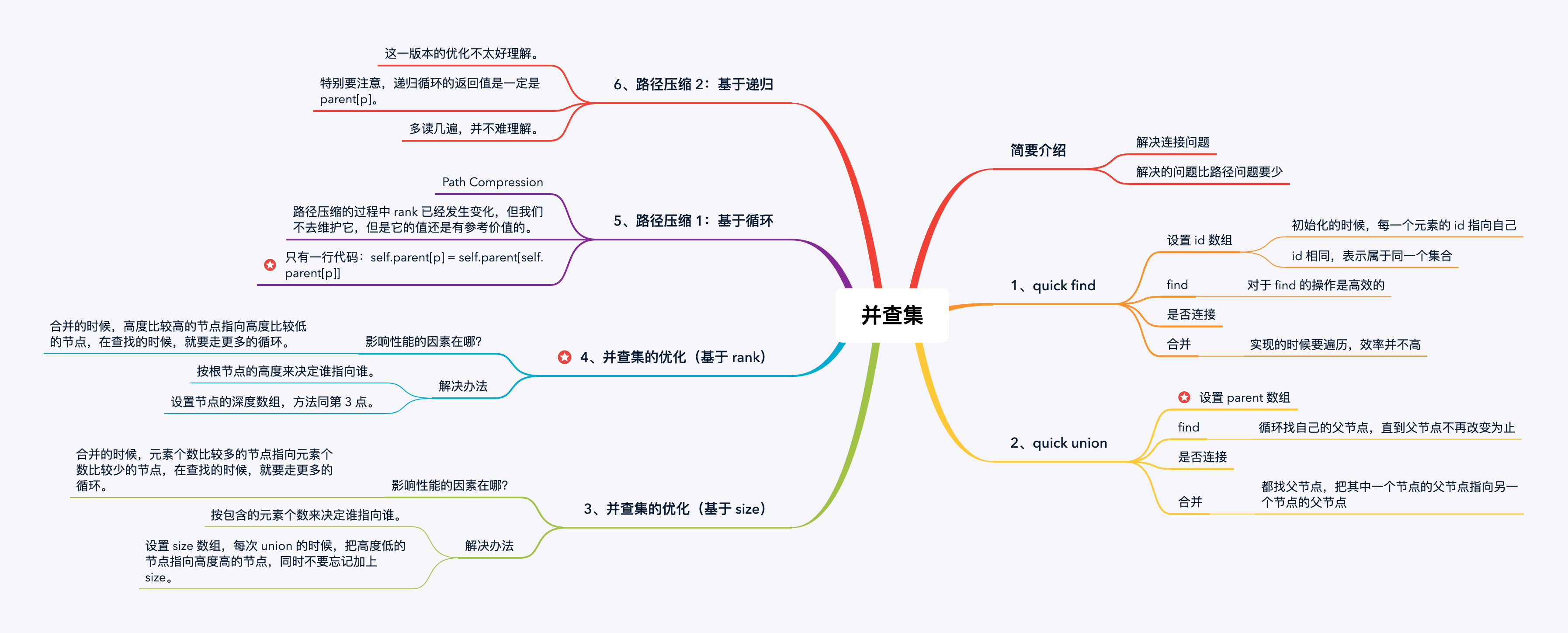
主要操作

并 Union

把两个集合合并成一个集合，表示这两个集合之间产生连接

查 Find

查询元素属于哪个集合

代码实现

代码框架

代码基本框架如下，对于find和union下面会介绍不同的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class UnionFind {
    int[] root;

    UnionFind(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    int find(int x) {
        return root[x];
    }

    void union(int x, int y) {
        // join x and y
    }

    boolean connected(int x, int y) {
        return find(x) == find(y);
    }
}

Quick Find 实现

此实现重点在于超快速find方法，时间复杂度在O(1)，而对于union时间复杂度是O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class UnionFindQuickFind extends UnionFind {
    UnionFindQuickFind(int size) {
        super(size);
    }

    int find(int x) {
        return root[x];
    }

    void union(int x, int y) {
        int rootX = find(x), rootY = find(y);
        if (rootX != rootY) {
            for (int i = 0; i < root.length; i++) {
                if (root[i] == rootY) {
                    root[i] = rootX;
                }
            }
        }
    }
}

Quick Union 实现

此实现是最常用的版本，其他的优化也是基于此版本
虽然提高了find方法的时间复杂度，但平均了union的时间复杂度，总体效率会高于Quick Find方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class UnionFindQuickUnion extends UnionFind {
    UnionFindQuickUnion(int size) {
        super(size);
    }

    int find(int x) {
        while (x != root[x]) {
            x = root[x];
        }
        return x;
    }

    void union(int x, int y) {
        int rootX = find(x), rootY = find(y);
        if (rootX != rootY) {
            root[rootY] = rootX;
        }
    }
}

按秩合并优化 实现

针对union操作的优化，在union操作时，根据约定的秩序从两个根节点中选择新的根结点

标准按秩，按当前树的高度合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class UnionFindOptimizationByRank extends UnionFindQuickUnion {
    int[] rank; // 新增rank数组， 存放当前root树的高度
    UnionFindOptimizationByRank(int size) {
        super(size);
        rank = new int[size];
        Arrays.fill(rank, 1); // 初始化，人人平等
    }

    void union(int x, int y) {
        int rootX = find(x), rootY = find(y);
        if (rootX == rootY) {
            return;
        }
        if (rank[rootX] > rank[rootY]) {
            root[rootY] = rootX;
        } else if (rank[rootY] > rank[rootX]) {
            root[rootX] = rootY;
        } else {
            root[rootY] = rootX;
            rank[rootX]++; // 增加高度
        }
    }
}

人多势众，按当前集合元素数量合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static class UnionFindOptimizationByCount extends UnionFindQuickUnion {
    int[] count;
    UnionFindOptimizationByCount(int size) {
        super(size);
        count = new int[size];
        Arrays.fill(count, 1); // 初始化，人人平等
    }

    void union(int x, int y) {
        int rootX = find(x), rootY = find(y);
        if (rootX == rootY) {
            return;
        }
        int newCount = count[rootX] + count[rootY];
        if (count[rootX] > count[rootY]) {
            root[rootY] = rootX;
            count[rootX] = newCount;
        } else {
            root[rootX] = rootY;
            count[rootY] = newCount;
        }
    }
}

路径压缩优化 实现

针对find操作的优化，在find操作时，压缩已查找的路径，具体实现有两种，差距不大

完全压缩（递归）

1
2
3
4
5
6
7
8
9
10
11
12
public static class UnionFindOptimizationPathUpdateComplete extends UnionFindQuickUnion {
    UnionFindOptimizationPathUpdateComplete(int size) {
        super(size);
    }

    int find(int x) {
        if (x == root[x]) {
            return x;
        }
        return root[x] = find(root[x]);
    }
}

隔代压缩（循环）

1
2
3
4
5
6
7
8
9
10
11
12
13
public static class UnionFindOptimizationPathUpdateGap extends UnionFindQuickUnion {
    UnionFindOptimizationPathUpdateGap(int size) {
        super(size);
    }

    int find(int x) {
        while (x != root[x]) {
            root[x] = root[root[x]];
            x = root[x];
        }
        return x;
    }
}

终极优化 版本

注：这里存在个人偏见
路径压缩优化后是否还需要按秩合并存在一丢丢的争议，读者可自行斟酌

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public static class UnionFindFinal {
    int[] root;
    int[] count;
    UnionFindFinal(int size) {
        count = new int[size];
        Arrays.fill(count, 1);
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    int find(int x) {
        while (x != root[x]) {
            root[x] = root[root[x]];
            x = root[x];
        }
        return x;
    }

    void union(int x, int y) {
        int rootX = find(x), rootY = find(y);
        if (rootX == rootY) {
            return;
        }
        int newCount = count[rootX] + count[rootY];
        if (count[rootX] > count[rootY]) {
            root[rootY] = rootX;
            count[rootX] = newCount;
        } else {
            root[rootX] = rootY;
            count[rootY] = newCount;
        }
    }

    boolean connected(int x, int y) {
        return find(x) == find(y);
    }
}

复杂度

Time Complexity: O(Nα(N)) ≈ O(N), where N is the number of vertices (and also the number of edges) in the graph, and α(N) is the Inverse-Ackermann function. We make up to N queries of dsu.union, which takes (amortized) O(α(N)) time.

Space Complexity: O(N)

刷题

常用方法

  1. 通过一些方法将自定义类型转为整型后使用并查集（e.g. 生成哈希值；二维变一维）
  2. 使用链表 + 映射（Map）
  3. 使用桩，stub

My Favorite

基本

变体

魔鬼

偷看答案

未解之谜

最小生成树

参考